PROJECT DESCRIPTION
INSTRUCTORS
SCHOOL SITE
LEVEL
SUBJECTS
ELECTRICITY USAGE
LESS THAN FIVE MATERIALS
TEACHERS NEEDED
BOOK CHAPTER

“Imagine Coachella times Physics. It was like a rave.”
Chris Wakefield was inspired by a Spanish artist, Ana Soler, who created an installation using thousands of tennis balls to illustrate the arcs of bouncing balls. But…she didn’t get the physics right!
Chris hoped his students would be inspired by the challenge of creating a similar exhibition, but getting the math and physics equations right. He launched the project by showing his students photos of the art installation and the somewhat daunting displacement equation Δx = Vo+ ½ at2. Several of his students were into composing electronic music, and they suggested adding a musical component to the work.
After the initial challenge, students spent the first week doing hands-on inquiry activities. Students dropped balls and caught them, documenting their position with the naked eye and photography. They experienced force as a feeling in their hands when catching balls dropped from varying heights. Then they made inferences about what they had seen and felt. Chris had a photography app that took bursts of photos at regular 0.1.second intervals and then stitched them together. They put these up on the screen and then used Google Draw to trace and measure vertical and horizontal distances of an object’s trajectory.
Want to see the whole project? Click the button to download the pages from the book that discuss this project!
Want to see the whole project? Click the button to download the pages from the book that discuss this project!
After getting a sense of the equation physically through experimentation, students spent the next two weeks learning the equation and practicing using it in real world problems. For example, “a punter kicks a football at an angle of 30° from the ground at an initial speed of 20 m/s. Where should a punt returner position themselves to catch the ball just before it strikes the ground? Also, what would be the maximum height of the ball?”
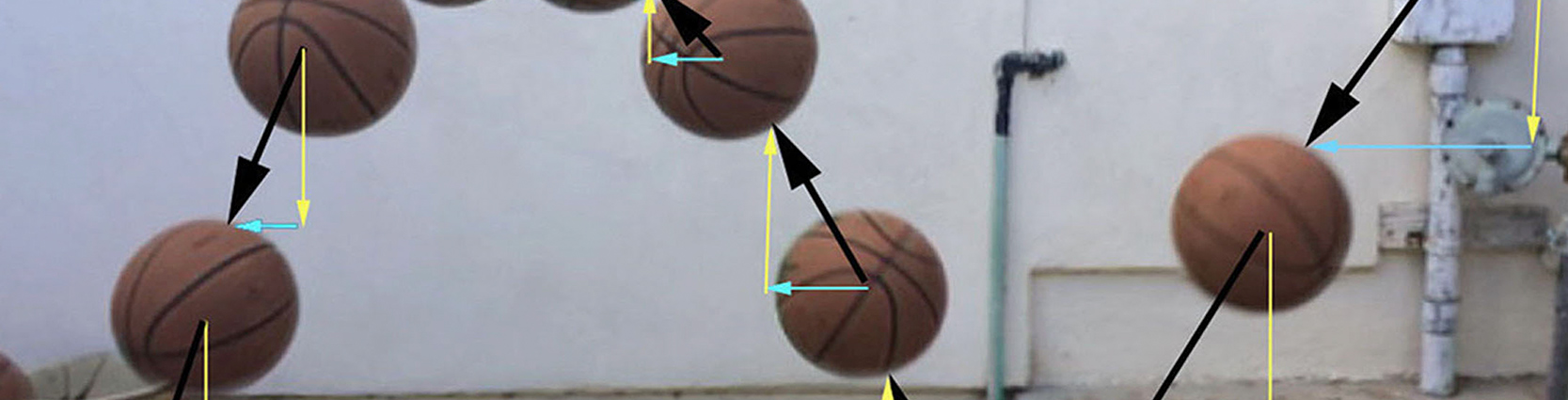
Chris built in Differentiation and allowed students to choose the level of challenge they wanted. For each level, students needed to do the calculations and create an installation showing the tennis ball’s trajectory. Three levels were offered:
Mild: Students calculated the horizontal displacement for an object moving at a constant velocity at 0.1 second intervals.
Medium: Students calculated the vertical displacement of an object in free fall at 0.1 second intervals.
Spicy: Students started by using trigonometry to determine the horizontal and vertical components of the initial velocity of an object launched at an angle. Using four variations of the displacement equation, students calculated the horizontal and vertical displacements of objects at calculated time intervals to show the parabolic nature of motion.
Once students had decided what they wanted to do, they paired up with others who had made the same choice. Chris advised them that the challenge option would require putting in some time during lunch and after school. Interestingly, there were several students who were a couple of years behind in math, but they still wanted to do the challenge option, because it looked like more fun.
Students painted tennis balls neon colors and used fishing line to hang them at heights that corresponded to their calculations. They blacked out the walls and used black lights, creating a rave atmosphere. Two students DJ’ed the exhibition with music they created. It was easy for students to self-assess their calculations, because if they were incorrect, the trajectory they displayed would not look right.
Students wrote up the calculations that informed their installations and displayed these outside the exhibition. They had to prepare a twenty second “elevator pitch” explaining the math, and a longer five minute explanation for those who were interested in hearing more.

